Nonlinear acoustic plane waves
The linear acoustics models describe most of the sound propagation situations from an human point of view. However, these models are only a simplification of what is really happening in the nature. For a more complete description of how acoustics waves propagates in fluids, one can take into account the nonlinear propagation effects.
Nonlinear harmonic travelling wave
In this simulations we show how a finite amplitude plane wave propagates through a viscous fluid. The propagation speed is amplitude dependent, and different from the small amplitude sound speed. Due to this, the wave compression peaks travel faster than the rarefaction minimum pressure, so the waves distorts as they travel. These steepening processes of the initial sinusoidal wave (i.e. only one spectral component) in frequency domain involves that the energy is transferred to higher harmonics. This effect is cumulative, so the frequency spectra (i.e. the spatiotemporal distortion of the wave) depends not only on the wave amplitude and frequency, but also on the propagated distance.

Time domain nonlinear acoustics propagation of a sinusoidal plane wave. The vertical line is at shock formation distance. This result was obtained by NL-FDTD method.
In this way, as the steepening develops, there is a distance where a discontinuity in the wave profile is formed (marked in the graphs with a vertical dashed line). This point is very useful to quantify and characterize nonlinear acoustics plane waves, and is named the shock distance:
\[z_{s}=\frac{c_0^2}{\omega _0(1+\frac{B}{2A})v_0} \]
where \(z_{s}\) is the shock distance, \(c_0\) is small amplitude sound speed and \(\frac{B}{A}\) is the nonlinear parameter of the media, \(\omega _0\) is the wave angular frequency and \(v_{max}\) is the particle velocity of the plane wave, related with the pressure \(p_0\) as \(v_0={p_0}/{\rho _0 c_0}\).

Time domain nonlinear acoustics propagation of a sinusoidal plane wave on a travelling reference system (the camera follows one cycle of the above signal). The initial harmonic waveform develops a shock wave (at the vertical line) and after that reach the sawtooth waveform regime.
Nonlinear single cycle travelling wave (N-wave)
When a single cycle of a wave is generated, special characteristics arises on the propagation. As the fist positive compression part of the wave propagates faster than the second rarefaction half, the wave develop steepening as the continuous sinusoidal case, until front and back shocks are formed.
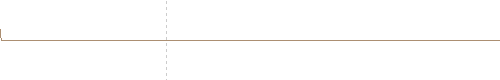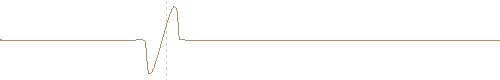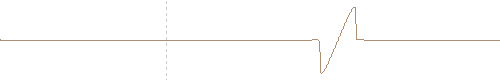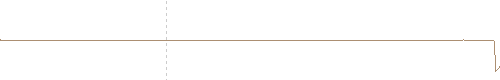
One dimensional FDTD computed nonlinear propagation of a single cycle plane wave. The initial sinusoidal waveform develops a N-wave.
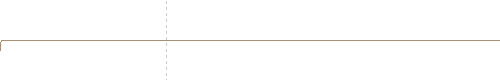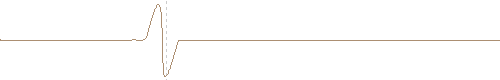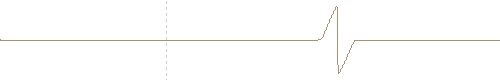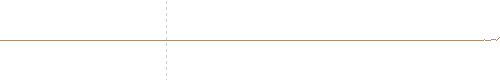
One dimensional FDTD computed nonlinear propagation of a inverted single cycle plane wave. The initial sinusoidal waveform develops a single shock wave.
However, the shock propagation speed depends on the jump conditions, i.e. the propagation speed of the top part and the bottom part of the discontinuity. Due to the different jump condition, different shock propagation speed is achieved. This effect spreads the single cycle in a longer effective wavelength. Thus, by simply changing the phase of the excitation (upper and lower graphs), completely different solutions are obtained due to the differences in the jump conditions.
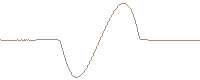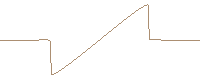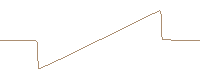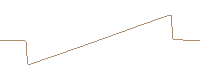
Single cycle sinusoidal wave developing a N-wave. (FDTD computed and travelling reference system)
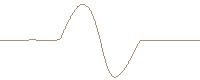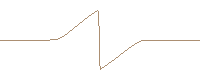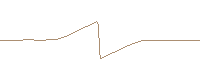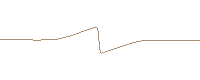
Inverted single cycle sinusoidal wave developing a single shock. (FDTD computed and travelling reference system)
Sonic booms
Sonic booms are created when an object travels faster than the speed of sound. At these speeds the high overpressure at the tip of the object and the rarefaction at the tail in supersonic speed form an acoustic shock wave. This wave rounds the object and creates a cone, similarly to the waves created by a canoe, but in 3D. After the formation, the wave propagates in nonlinear regime as the N-waves described above. These objects are commonly planes in supersonic flight, but any object can create a sonic boom: actually, the characteristic sound of a bullwhip crack is due to the supersonic speed of the tip that creates a "mini" sonic boom.
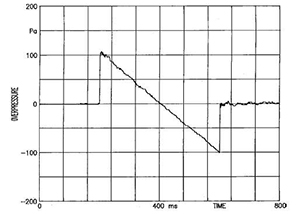
Sonic-boom waveform of Columbia space shuttle, recorded at landing 10 December 1990. [Robert W. Young, "Sonic booms of space shuttles approaching Edwards Air Force Base, 1988–1993", J. Acoust. Soc. Am. 111 (1) 569, 2002]

Endeavour space shuttle breaking the sound barrier during the take off. The sonic boom is created not only at the moment of breaking the barrier, but also during all the supersonic flight.