Acoustic streaming in a resonator
When linear sound is considered, the particle vibration of the media con be considered as as pure harmonic (i. e. the period average velocity is zero). However, if we retain the nonlinearity of the medium and dissipation effects as in real acoustic media, the particles exhibit a period average velocity. This means when an acoustic beam propagates trough a medium, the medium responds with a continuous flow, also called acoustic streaming or "quartz wind" in case of air.
Acoustic streaming in resonating cavities
In the case of a acoustic resonator, some diverse stream patterns could be observed. In the image below is shown a nonlinear acoustics axisymmetric FDTD simulation result or a nonlinear ultrasound plane source, showing the mean flow created by the acoustic wave. In the background color, nonlinear acoustic pressure envelope field is plotted. Thus, for a cavity of length \(2\lambda\) the flow in the axis of the source travels away and return from the external layer. In this simulations the cavity was filled with glycerol (\(c_0=1904\)m/s, \(\rho _0=1261\) kg/m3, \(\eta=1.4\), Pa/s \(\frac{B}{2A}=9.1\)) and the source is a plane transducer \(f_0=1\) MHz.
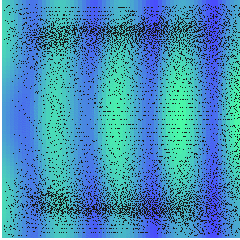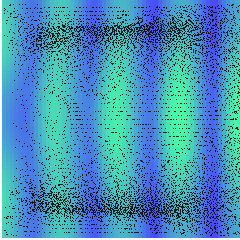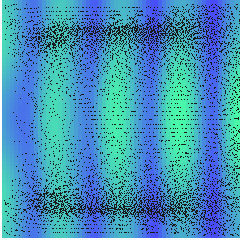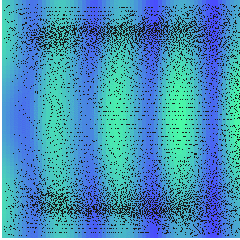
Computed streaming in an acoustic resonator \(z=2\lambda\), \(r=2\lambda\), \(Z_{wall}=5Z_{0}\) and \(p_{0}=1\)MPa
However, if the wall impedance change \(Z_{wall}=20Z_{0}\)and amplitude of the acoustic wave \(p_{0}=8\)MPa is increased, the stream can be modified as we show below. Here, the confined stream shows two pair of vortex.
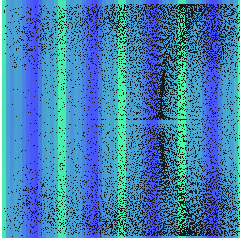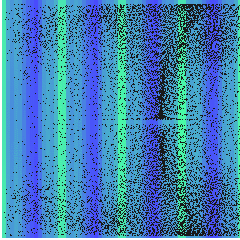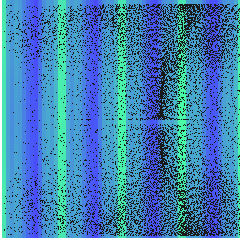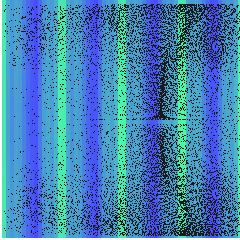
Computed streaming in an acoustic resonator \(z=2\lambda\), \(r=2\lambda\), \(Z_{wall}=20Z_{0}\) and \(p_{0}=8\) MPa
And in a long resonator, more complex stream appears:
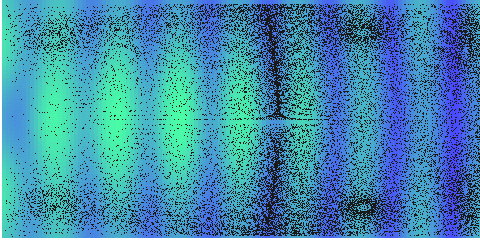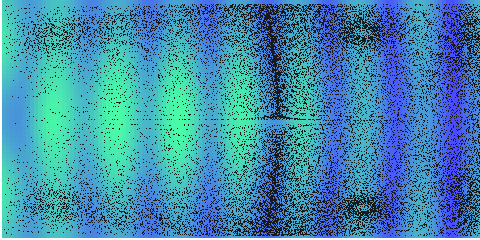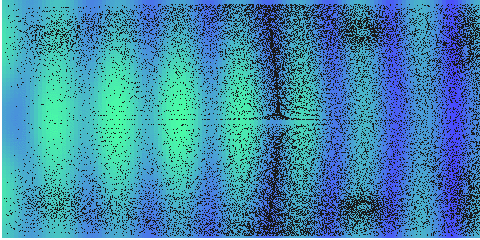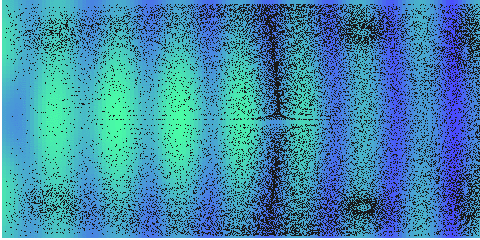
Computed streaming in an acoustic resonator \(z=4\lambda\), \(r=2\lambda\), \(Z_{wall}=20Z_{0}\) and \(p_{0}=8\) MPa
Acoustic streaming in free boundary resonator
If continuity is fixed at one side of the resonator \(\frac{\partial{v_z}}{\partial z} =0|_{z_{max}}\), the streaming pattern changes completely. As a free boundary, the velocity out of the resonator is equal to the velocity inside it, so the outer media can act like a mass source.
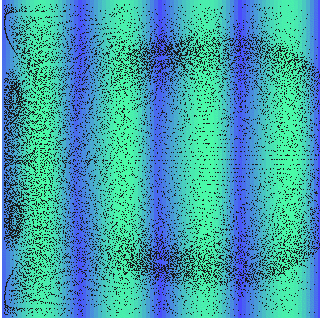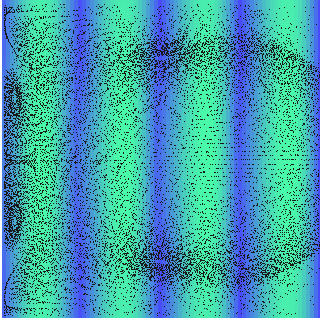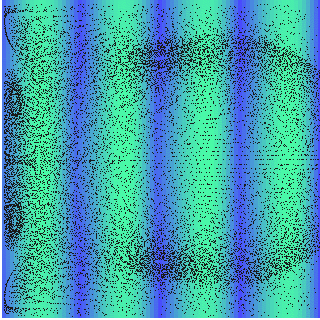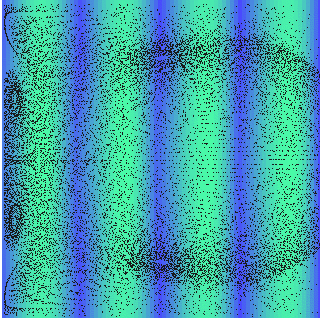
Computed streaming in an free boundary acoustic resonator \(z=2\lambda\), \(r=2\lambda\), \(Z_{wall}=20Z_{0}\) and \(p_{0}=60\) MPa