Focused acoustic sources
When an acoustic radiator presents a curved surface, the acoustic field presents a natural focusing. However, due to the diffractive effects of the acoustic waves, the focalization isn't is a perfect spot. Thus, the focusing properties (i. e. the gain, the beamwidth or the focus location) strongly depends on diffraction. In this way, as the wavelength is comparable to the source aperture the the location of the maximum peak pressure get close the geometrical focus. In addition, the gain of the transducer and the focus beamwidth change too as the source \(f_{number}\) changes or the source frequency varies. For a source of aperture \(A\), focal \(F\) and angular frequency \(\omega\) we can define the \(f_{number}\) as:
\[f_{number} = \frac{A}{F}\]
3D acoustic volume rendering for focused sources

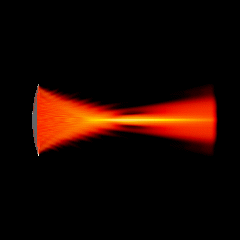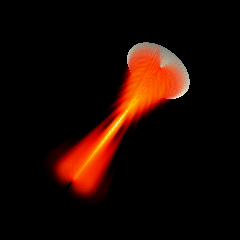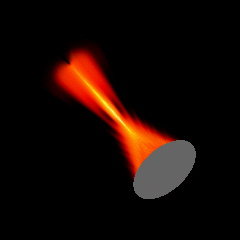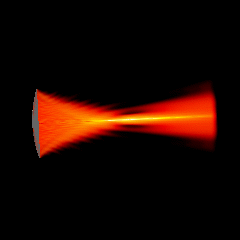
Acoustic focused sources fields for \(f_{number} = 5\) and \(f_{number} = 3\)
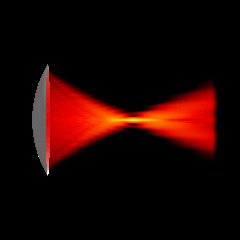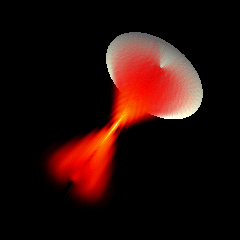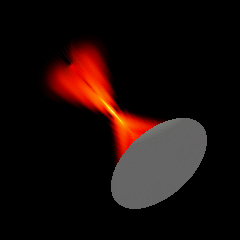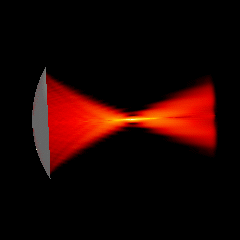
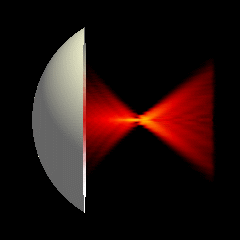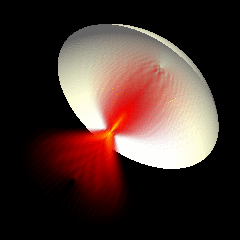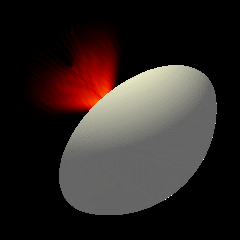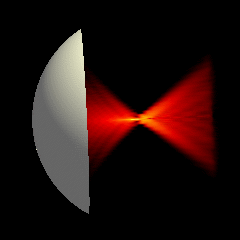
Acoustic focused sources fields for \(f_{number} = 2\) and \(f_{number} = 1.25\)
Focused source for \(f_{number} = 5\)

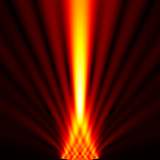
Focused source for \(f_{number} = 3\)

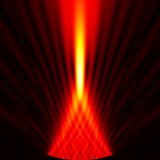
Focused source for \(f_{number} = 2\)

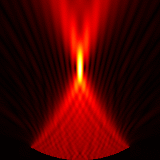
Focused source for \(f_{number} = 1.25\)

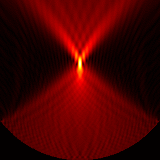
Analytic description
Some basic relations describe the acoustic field of a focusing source, thus, this relation shows the focusing degree of the source. For obtain the transducer gain, defined as the relation of the pressure in the transducer surface and the pressure measured at the focal we can show for small amplitude acoustic waves the following relation:
\[G=\frac{L_d}{F}\]
where the Rayleigh distance is defined as:
\[L_d=\frac{k (\frac{A}{2})^2}{2}\]
Another interesting parameter that characterize the source is the Fresnel number \(N_f\), defined as:
\[N_f=\frac{G}{\pi}\]
Finally, the pressure modulus over the axis \(z\) for a focused source as:
\[p(0,\tilde{z})=p_0\left|{\frac{2}{1-\tilde{z}}\sin\left({\frac{\pi N_f({1-\tilde{z}})}{2\tilde{z}}}\right)}\right|\]
where \( p_0\) is the pressure at the transducers surface and \(\tilde{z}=\frac{z}{F}\) is the normalized axial coordinate.